
Introduction
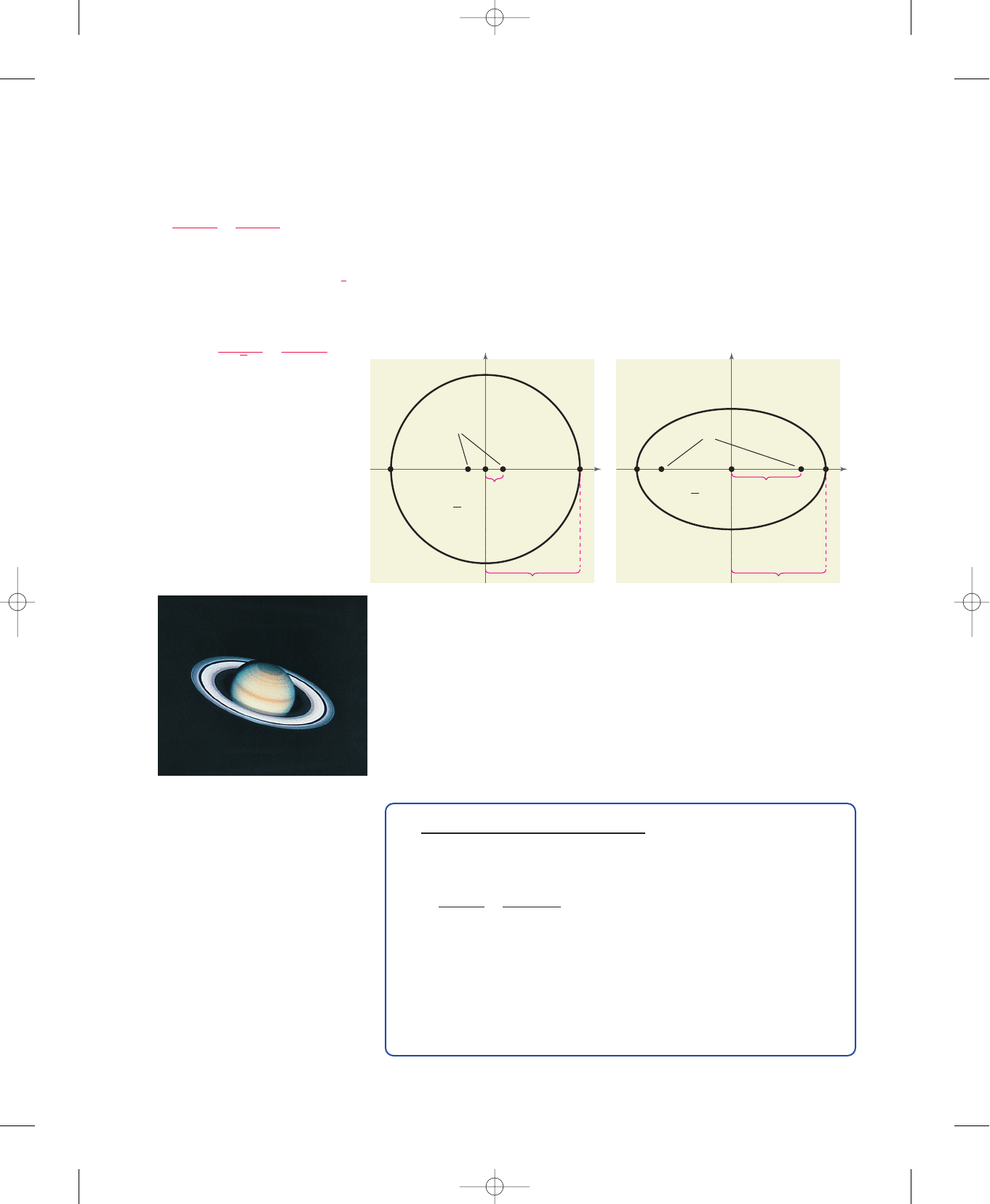
The second type of conic is called an ellipse, and is defined as follows.
is constant.
FIGURE 10.18 FIGURE 10.19
The line through the foci intersects the ellipse at two points called vertices.
The chord joining the vertices is the major axis, and its midpoint is the center
of the ellipse. The chord perpendicular to the major axis at the center is the
minor axis of the ellipse. See Figure 10.19.
You can visualize the definition of an ellipse by imagining two thumbtacks
placed at the foci, as shown in Figure 10.20. If the ends of a fixed length of string
are fastened to the thumbtacks and the string is drawn taut with a pencil, the path
traced by the pencil will be an ellipse.
FIGURE 10.20
To derive the standard form of the equation of an ellipse, consider the ellipse
in Figure 10.21 with the following points: center, vertices, foci,
Note that the center is the midpoint of the segment joining the foci.
h
±
c, k
.
h
±
a, k
;
h, k
;
d
1
d
2
Major axis
Minor
axis
Center
Vertex
Vertex
Focus
Focus
(x, y)
d
d
2
1
744 Chapter 10 Topics in Analytic Geometry
What you should learn
•Write equations of ellipses
in standard form and graph
ellipses.
•Use properties of ellipses
to model and solve real-life
problems.
•Find eccentricities of ellipses.
Why you should learn it
Ellipses can be used to model
and solve many types of
real-life problems. For instance,
in Exercise 59 on page 751, an
ellipse is used to model the orbit
of Halley’s comet.
Ellipses
Harvard College Observatory/
SPL/Photo Researchers, Inc.
10.3
Definition of Ellipse
An ellipse is the set of all points in a plane, the sum of whose
distances from two distinct fixed points (foci) is constant. See Figure 10.18.
x, y
b
a
c
(, )h k
(, )
x y
bc
22
+
bc
22
+
2 b
2
+ c
2
= 2a
b
2
+ c
2
= a
2
FIGURE 10.21
333202_1003.qxd 12/8/05 9:01 AM Page 744

The sum of the distances from any point on the ellipse to the two foci is constant.
Using a vertex point, this constant sum is
Length of major axis
or simply the length of the major axis. Now, if you let be any point on the
ellipse, the sum of the distances between and the two foci must also be
That is,
Finally, in Figure 10.21, you can see that which implies that the
equation of the ellipse is
You would obtain a similar equation in the derivation by starting with a
vertical major axis. Both results are summarized as follows.
Figure 10.22 shows both the horizontal and vertical orientations for an ellipse.
Major axis is horizontal. Major axis is vertical.
FIGURE 10.22
x
(x − h)
2
(y − k)
2
2
b
2
a
+= 1
2a
2b
(h, k)
y
(x − h)
2
(y − k)
2
2
a
2
b
+= 1
2a
2b
(h, k)
y
x
x h
2
a
2
y k
2
b
2
1.
b
2
x h
2
a
2
y k
2
a
2
b
2
b
2
a
2
c
2
,
x
h c
2
y k
2
x
h c
2
y k
2
2a.
2a.
x, y
x, y
a c
a c
2a
Section 10.3 Ellipses 745
When discussing ellipses, you might also
choose to discuss the latera recta as
background for Exercises 62–66.
Consider the equation of the
ellipse
If you let then the equa-
tion can be rewritten as
which is the standard form of
the equation of a circle with
radius (see Section 1.2).
Geometrically, when for
an ellipse, the major and minor
axes are of equal length, and so
the graph is a circle.
a b
r a
x h
2
y k
2
a
2
a b,
x h
2
a
2
y k
2
b
2
1.
Standard Equation of an Ellipse
The standard form of the equation of an ellipse, with center and
major and minor axes of lengths and respectively, where is
Major axis is horizontal.
Major axis is vertical.
The foci lie on the major axis, units from the center, with
If the center is at the origin the equation takes one of the following
forms.
x
2
b
2
y
2
a
2
1
x
2
a
2
y
2
b
2
1
0, 0
,
c
2
a
2
b
2
.c
x h
2
b
2
y k
2
a
2
1.
x h
2
a
2
y k
2
b
2
1
0
<
b
<
a,2b,2a
h, k
Major axis is
horizontal.
Major axis is
vertical.
333202_1003.qxd 12/8/05 9:01 AM Page 745

Finding the Standard Equation of an Ellipse
Find the standard form of the equation of the ellipse having foci at and
and a major axis of length 6, as shown in Figure 10.23.
Solution
Because the foci occur at and the center of the ellipse is and
the distance from the center to one of the foci is Because you
know that Now, from you have
Because the major axis is horizontal, the standard equation is
This equation simplifies to
Now try Exercise 49.
Sketching an Ellipse
Sketch the ellipse given by
Solution
Begin by writing the original equation in standard form. In the fourth step, note
that 9 and 4 are added to both sides of the equation when completing the squares.
Write original equation.
Group terms.
Factor 4 out of y-terms.
Write in completed square form.
Divide each side by 4.
Write in standard form.
From this standard form, it follows that the center is Because
the denominator of the -term is the endpoints of the major axis lie two
units to the right and left of the center. Similarly, because the denominator of the
-term is the endpoints of the minor axis lie one unit up and down from
the center. Now, from you have So, the
foci of the ellipse are and The ellipse is shown in
Figure 10.24.
Now try Exercise 25.
3
3, 1
.
3
3, 1
c
2
2
1
2
3.c
2
a
2
b
2
,
b
2
1
2
,y
a
2
2
2
,x
h, k
3, 1
.
x 3
2
2
2
y 1
2
1
2
1
x 3
2
4
y 1
2
1
1
x 3
2
4
y 1
2
4
x
2
6x 9
4
y
2
2y 1
9 9 4
1
x
2
6x
4
y
2
2y
9
x
2
6x
4y
2
8y
9
x
2
4y
2
6x 8y 9 0
x
2
4y
2
6x 8y 9 0.
x 2
2
9
y 1
2
5
1.
x 2
2
3
2
y 1
2
5
2
1.
b
a
2
c
2
3
2
2
2
5.
c
2
a
2
b
2
,a 3.
2a 6,c 2.
2, 1)
4, 1
,
0, 1
4, 1
0, 1
746 Chapter 10 Topics in Analytic Geometry
Remind your students that completing
the square must be performed twice to
write the equation of the ellipse in
standard form in Example 2.
1
3
−1
3
4
(2, 1)(0, 1) (4, 1)
b = 5
a = 3
−1
−2
y
x
FIGURE 10.23
x
−1−3− 4−5
− 1
1
2
3
4
(−3, 1)
(−3, 2)
(−3, 0)
(−5, 1)
(−1, 1)
(3)x +
2
+
= 1
2
2
1
2
(1)y −
2
y
3, 1− 3 −
( )
( )
3, 1− 3 +
FIGURE 10.24
Example 1
Example 2
333202_1003.qxd 12/8/05 9:01 AM Page 746

Analyzing an Ellipse
Find the center, vertices, and foci of the ellipse
Solution
By completing the square, you can write the original equation in standard form.
Write original equation.
Group terms.
Factor 4 out of terms.
Write in completed square form.
Divide each side by 16.
Write in standard form.
The major axis is vertical, where and
So, you have the following.
Center: Vertices: Foci:
The graph of the ellipse is shown in Figure 10.25.
Now try Exercise 29.
1, 2 2
3
1, 2
1, 2 2
3
1, 6
1, 2
c
a
2
b
2
16 4
12 2
3.
h 1, k 2, a 4, b 2,
x 1
2
2
2
y 2
2
4
2
1
x 1
2
4
y 2
2
16
1
4
x 1
2
y 2
2
16
4
x
2
2x 1
y
2
4y 4
8 4
1
4
x- 4
x
2
2x
y
2
4y
8
4x
2
8x
y
2
4y
8
4 x
2
y
2
8x 4y 8 0
4x
2
y
2
8x 4y 8 0.
Section 10.3 Ellipses 747
Example 3
−4 −224
2
Vertex
Vertex
Focus
Focus
Center
(1, 6)−
(1, 2)
(1, 2)−
1, 2 2 3−−
1, 2 + 2 3−
(
(
(
(
+= 1
y
x
2
2
(x − 1)
2
4
2
(y + 2)
2
FIGURE 10.25
You can use a graphing utility to graph an ellipse by graphing the upper and
lower portions in the same viewing window. For instance, to graph the ellipse in
Example 3, first solve for to get
and
Use a viewing window in which and You should obtain
the graph shown below.
−69
−7
3
7
≤
y
≤
3.6
≤
x
≤
9
y
2
2 4
1
x 1
2
4
.y
1
2 4
1
x 1
2
4
y
Technology
333202_1003.qxd 12/8/05 9:01 AM Page 747

Application
Ellipses have many practical and aesthetic uses. For instance, machine gears,
supporting arches, and acoustic designs often involve elliptical shapes. The orbits
of satellites and planets are also ellipses. Example 4 investigates the elliptical
orbit of the moon about Earth.
An Application Involving an Elliptical Orbit
The moon travels about Earth in an elliptical orbit with Earth at one focus, as
shown in Figure 10.26. The major and minor axes of the orbit have lengths of
768,800 kilometers and 767,640 kilometers, respectively. Find the greatest and
smallest distances (the apogee and perigee), respectively from Earth’s center to
the moon’s center.
Solution
Because and you have
and
which implies that
So, the greatest distance between the center of Earth and the center of the moon
is
kilometers
and the smallest distance is
kilometers.
Now try Exercise 59.
Eccentricity
One of the reasons it was difficult for early astronomers to detect that the orbits
of the planets are ellipses is that the foci of the planetary orbits are relatively
close to their centers, and so the orbits are nearly circular. To measure the
ovalness of an ellipse, you can use the concept of eccentricity.
Note that for every ellipse.0
<
e
<
1
a c 384,400 21,108 363,292
a c 384,400 21,108 405,508
21,108.
384,400
2
383,820
2
c
a
2
b
2
b 383,820a 384,400
2b 767,640,2a 768,800
748 Chapter 10 Topics in Analytic Geometry
Example 4
Definition of Eccentricity
The eccentricity of an ellipse is given by the ratio
e
c
a
.
e
Ask students to make a conjecture
about the eccentricity of a circle before
going further.
Perigee
Moon
Apogee
Earth
768,800
km
767,640
km
FIGURE 10.26
Note in Example 4 and Figure
10.26 that Earth is not the center
of the moon’s orbit.
333202_1003.qxd 12/8/05 9:01 AM Page 748
To see how this ratio is used to describe the shape of an ellipse, note that
because the foci of an ellipse are located along the major axis between the vertices
and the center, it follows that
For an ellipse that is nearly circular, the foci are close to the center and the ratio
is small, as shown in Figure 10.27. On the other hand, for an elongated
ellipse, the foci are close to the vertices, and the ratio is close to 1, as shown
in Figure 10.28.
FIGURE 10.27 FIGURE 10.28
The orbit of the moon has an eccentricity of and the eccentricities
of the nine planetary orbits are as follows.
Mercury: Saturn:
Venus: Uranus:
Earth: Neptune:
Mars: Pluto:
Jupiter: e 0.0484
e 0.2488e 0.0934
e 0.0086e 0.0167
e 0.0472e 0.0068
e 0.0542e 0.2056
e 0.0549,
ca
ca
0
<
c
<
a.
Section 10.3 Ellipses 749
Foci
e is small.
a
c
e =
c
a
x
y
Foci
a
c
x
y
e is close to 1.
e =
c
a
W
RITING ABOUT
M
AT H EMATICS
Ellipses and Circles
a. Show that the equation of an ellipse can be written as
b. For the equation in part (a), let and and use a graphing
utility to graph the ellipse for and
Discuss the changes in the shape of the ellipse as approaches 0.
c. Make a conjecture about the shape of the graph in part (b) when What
is the equation of this ellipse? What is another name for an ellipse with an
eccentricity of 0?
e 0.
e
e 0.1.
e 0.25,e 0.5,e 0.75,e 0.95,
k 2,h 1,a 4,
x h
2
a
2
y k
2
a
2
1 e
2
1.
The time it takes Saturn to orbit the
sun is equal to 29.4 Earth years.
NASA
Activities
1. Find the center, foci, vertices, and
eccentricity of the ellipse
Answer: Center
Foci
Vertices
2. Rewrite the equation of the ellipse in
standard form:
Answer:
x 2
2
5
2
y 3
2
3
2
1
9x
2
5y
2
36x 30y 36 0.
e
4
5
3, 1
,
7, 1
;
6, 1
;
2, 1
,
2, 1
;
x 2
2
25
y 1
2
9
1.
333202_1003.qxd 12/8/05 9:01 AM Page 749

In Exercises 1–6, match the equation with its graph. [The
graphs are labeled (a), (b), (c), (d), (e), and (f).]
(a) (b)
(c) (d)
(e) (f)
1. 2.
3. 4.
5.
6.
In Exercises 7–30, identify the conic as a circle or an ellipse.
Then find the center, radius, vertices, foci, and eccentricity
of the conic (if applicable), and sketch its graph.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
In Exercises 31–34, use a graphing utility to graph the
ellipse. Find the center, foci, and vertices. (Recall that it may
be necessary to solve the equation for and obtain two
equations.)
31. 32.
33.
34. 36x
2
9y
2
48x 36y 72 0
12x
2
20y
2
12x 40y 37 0
3x
2
4y
2
125x
2
3y
2
15
y
16x
2
16y
2
64x 32y 55 0
9x
2
25y
2
36x 50y 60 0
16x
2
25y
2
32x 50y 16 0
9x
2
9y
2
18x 18y 14 0
x
2
y
2
4x 6y 3 0
x
2
4y
2
6x 20y 2 0
6x
2
2y
2
18x 10y 2 0
3x
2
y
2
18x 2y 8 0
x
2
5y
2
8x 30y 39 0
x
2
y
2
2x 4y 31 0
9x
2
4y
2
54x 40y 37 0
9x
2
4y
2
36x 24y 36 0
x 3
2
254
y 1
2
254
1
x 2
2
y 4
2
14
1
x 5
2
94
y 1
2
1
x
2
49
y 1
2
49
1
x 4
2
12
y 3
2
16
1
x 3
2
16
y 5
2
25
1
x
2
64
y
2
28
1
x
2
5
y
2
9
1
x
2
9
y
2
9
1
x
2
25
y
2
25
1
x
2
81
y
2
144
1
x
2
25
y
2
16
1
x 2
2
9
y 2
2
4
1
x 2
2
16
y 1
2
1
x
2
4
y
2
4
1
x
2
4
y
2
25
1
x
2
9
y
2
4
1
x
2
4
y
2
9
1
−4
−4
4
4
x
y
−6
−6
2−2
−2
2
x
y
−4
−6
46
2
6
x
y
−4
−4
42
4
y
x
−4
−4
4
2
4
x
y
x
−
4
42
2
y
750 Chapter 10 Topics in Analytic Geometry
Exercises 10.3
VOCABULARY CHECK: Fill in the blanks.
1. An ________ is the set of all points in a plane, the sum of whose distances from two distinct fixed points, called
________, is constant.
2. The chord joining the vertices of an ellipse is called the ________ ________, and its midpoint is the ________ of the ellipse.
3. The chord perpendicular to the major axis at the center of the ellipse is called the ________ ________ of the ellipse.
4. The concept of ________ is used to measure the ovalness of an ellipse.
PREREQUISITE SKILLS REVIEW: Practice and review algebra skills needed for this section at www.Eduspace.com.
x, y
333202_1003.qxd 12/8/05 9:01 AM Page 750

Section 10.3 Ellipses 751
In Exercises 35–42, find the standard form of the equation
of the ellipse with the given characteristics and center at
the origin.
35. 36.
37. Ve rtices: foci:
38. Ve rtices: foci:
39. Foci: major axis of length 12
40. Foci: major axis of length 8
41. Ve rtices: passes through the point
42. Major axis vertical; passes through the points and
In Exercises 43–54, find the standard form of the equation
of the ellipse with the given characteristics.
43. 44.
45. 46.
47. Ve rtices: minor axis of length 2
48. Foci: major axis of length 8
49. Foci: major axis of length 16
50. Center: vertex: minor axis of length 2
51. Center: vertices:
52. Center: foci:
53. Ve rtices: endpoints of the minor axis:
54. Ve rtices: endpoints of the minor axis:
55. Find an equation of the ellipse with vertices and
eccentricity
56. Find an equation of the ellipse with vertices and
eccentricity
57. Architecture A semielliptical arch over a tunnel for a
one-way road through a mountain has a major axis of
50 feet and a height at the center of 10 feet.
(a) Draw a rectangular coordinate system on a sketch of
the tunnel with the center of the road entering the
tunnel at the origin. Identify the coordinates of the
known points.
(b) Find an equation of the semielliptical arch over the
tunnel.
(c) You are driving a moving truck that has a width of
8 feet and a height of 9 feet. Will the moving truck
clear the opening of the arch?
58. Architecture A fireplace arch is to be constructed in the
shape of a semiellipse. The opening is to have a height of
2 feet at the center and a width of 6 feet along the base (see
figure). The contractor draws the outline of the ellipse
using tacks as described at the beginning of this section.
Give the required positions of the tacks and the length of
the string.
−1−2−3123
1
3
− 2
4
x
y
e
1
2
.
0,
±
8
e
3
5
.
±
5, 0
1, 6
,
9, 6
5, 0
,
5, 12
;
2, 3
,
2, 1
0, 2
,
4, 2
;
1, 2
,
5, 2
3, 2
; a 3c;
4, 4
,
4, 4
0, 4
; a 2c;
2,
1
2
;
2, 1
;
0, 0
,
0, 8
;
0, 0
,
4, 0
;
0, 4
,
4, 4
;
−1
(2, −2)
(0, −1)
(4, −1)
(2, 0)
132
1
−1
−2
−3
−4
x
y
(2, 0)−
(2, 3)
(2, 6)−
(6, 3)−
2
2
−6
8
4
−4 4
y
x
4
−4
3
−3
−2
−1
2
1
x
(4, 4)
(7, 0)
(1, 0)
(4, −4)
352468
y
4
432
5
5
6
6
3
2
1
1
(2, 6)
(1, 3)
(3, 3)
(2, 0)
x
y
2, 0
0, 4
4, 2
0,
±
5
;
±
2, 0
;
±
5, 0
;
0,
±
4
0,
±
8
;
±
2, 0
±
6, 0
;
x
4−4
−4
4
( )
()
(−2, 0) (2, 0)
3
3
2
2
0,
0, −
y
4−4−88
−8
8
(0, 4)
(0, 4)−
(2, 0)− (2, 0)
x
y
59. Comet Orbit Halley’s comet has an elliptical orbit,
with the sun at one focus. The eccentricity of the orbit
is approximately 0.967. The length of the major axis of
the orbit is approximately 35.88 astronomical units.
(An astronomical unit is about 93 million miles.)
(a) Find an equation of the orbit. Place the center of the
orbit at the origin, and place the major axis on the
-axis.
(b) Use a graphing utility to graph the equation of the
orbit.
(c) Find the greatest (aphelion) and smallest (perihelion)
distances from the sun’s center to the comet’s center.
x
Model It
333202_1003.qxd 12/8/05 9:01 AM Page 751

60. Satellite Orbit The first artificial satellite to orbit Earth
was Sputnik I (launched by the former Soviet Union in
1957). Its highest point above Earth’s surface was
947 kilometers, and its lowest point was 228 kilometers
(see figure). The center of Earth was the focus of the
elliptical orbit, and the radius of Earth is 6378 kilometers.
Find the eccentricity of the orbit.
61. Motion of a Pendulum The relation between the velocity
(in radians per second) of a pendulum and its angular
displacement from the vertical can be modeled by a
semiellipse. A 12-centimeter pendulum crests
when the angular displacement is radian and
0.2 radian. When the pendulum is at equilibrium
the velocity is radians per second.
(a) Find an equation that models the motion of the
pendulum. Place the center at the origin.
(b) Graph the equation from part (a).
(c) Which half of the ellipse models the motion of the
pendulum?
62. Geometry A line segment through a focus of an ellipse
with endpoints on the ellipse and perpendicular to the
major axis is called a latus rectum of the ellipse.
Therefore, an ellipse has two latera recta. Knowing the
length of the latera recta is helpful in sketching an ellipse
because it yields other points on the curve (see figure).
Show that the length of each latus rectum is
In Exercises 63–66, sketch the graph of the ellipse, using
latera recta (see Exercise 62).
63. 64.
65. 66.
Synthesis
True or False? In Exercises 67 and 68, determine whether
the statement is true or false. Justify your answer.
67. The graph of is an ellipse.
68. It is easier to distinguish the graph of an ellipse from the
graph of a circle if the eccentricity of the ellipse is large
(close to 1).
69. Exploration Consider the ellipse
(a) The area of the ellipse is given by Write the
area of the ellipse as a function of
(b) Find the equation of an ellipse with an area of
264 square centimeters.
(c) Complete the table using your equation from part (a),
and make a conjecture about the shape of the ellipse
with maximum area.
(d) Use a graphing utility to graph the area function and
use the graph to support your conjecture in part (c).
70. Think About It At the beginning of this section it was
noted that an ellipse can be drawn using two thumbtacks, a
string of fixed length (greater than the distance between the
two tacks), and a pencil. If the ends of the string are
fastened at the tacks and the string is drawn taut with a
pencil, the path traced by the pencil is an ellipse.
(a) What is the length of the string in terms of
(b) Explain why the path is an ellipse.
Skills Review
In Exercises 71–74, determine whether the sequence is
arithmetic, geometric, or neither.
71. 80, 40, 20, 10, 5, . . . 72. 66, 55, 44, 33, 22, . . .
73. . . . 74. 1, 2, 4, . . .
In Exercises 75–78, find the sum.
75. 76.
77. 78.
10
n 1
4
3
4
n 1
10
n 0
5
4
3
n
6
n 0
3
n
6
n 0
3
n
1
2
,
1
4
,
7
2
,
5
2
,
3
2
,
1
2
,
1
2
,
a?
a.
A
ab.
a b 20.
x
2
a
2
y
2
b
2
1,
x
2
4y
4
4 0
9x
2
4y
2
365x
2
3y
2
15
x
2
4
y
2
1
1
x
2
9
y
2
16
1
x
F
1
F
2
Latera recta
y
2b
2
a.
1.6
0
,
0.2
y 0
y
228 km
947 km
Focus
752 Chapter 10 Topics in Analytic Geometry
a 891011 12 13
A
333202_1003.qxd 12/8/05 9:01 AM Page 752
